Lernauftrag 12: Zusammenhang P und W
Hier findest du die Aufgaben ohne Lösungen.
Die Kochplatte eines Elektroherdes ist ein Energieumwandlungssystem. Elektrische Energie wird genutzt, um Wärmeenergie zu erzeugen.
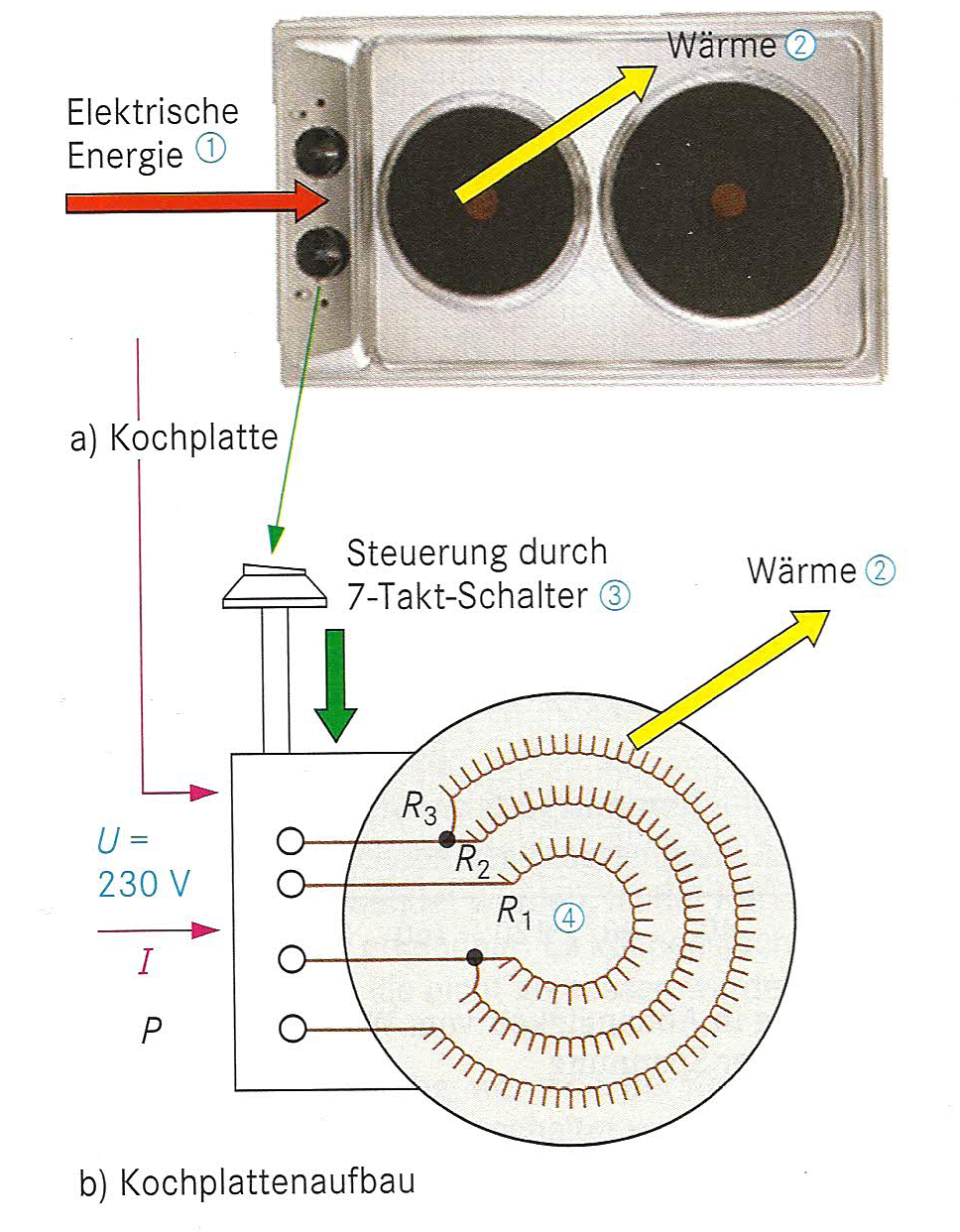
Aufgabe 1
Lies den folgenden Textabschnitt und ergründe, welche elektrischen Größen in die Lücken gehört.
Die Steuerung des Energieflusses geschieht mit Hilfe eines Schalters, der 7 Stellungen besitzt (7-Takt-Schalter).
Für alle Heizstufen wird die gleiche Netzspannung von \(U=230\ V\) benutzt.
- Bei der kleinsten Heizstufe ist der Strom am kleinsten.
- Bei der größten Heizstufe ist der Strom am größten.
Jede Schalterstufe liefert also eine andere Heizleistung, die durch die Zusammenschaltung der drei Heizwiderstände bestimmt wird.
Auf elektrischen Energiewandlern findet man in der Regel eine Leistungsangabe. Mit dieser Größe kennzeichnet man die Wirksamkeit der elektrischen Energieumwandlung.
Voraussetzung für elektrische Leistung ist, dass Strom \(I\) und Spannung \(U\) vorhanden sind.
Aufgabe 2
Finde und notiere die Gleichung zur Berechnung der elektrischen Leistung.
\(P = U\cdot I\)
Der Formelzeichen der Leistung ist \(P\) (von engl. power).
Die Einheiten der Leistung \(P\) sind \(W = V\cdot A = VA = J/s\)
Aufgabe 3
Lies den folgenden Textabschnitt und ergründe, welche elektrischen Größen in die Lücken gehören.
Die elektrische Energie, die der Kochplatte zugeführt wird, muss bezahlt werden. Der Betrieb mit kleiner Heizleistung kostet weniger als der mit voller Heizleistung. Die Energiemenge, die den Verbrauchspreis ausmacht, steigt außerdem mit der Betriebsdauer.
Die zugeführte elektrische Energie ist deshalb abhängig von der Leistung \(P\) und der Zeit \(t\).
Aufgabe 4
Finde und notiere die Gleichung zur Berechnung der elektrischen Energie.
\(W_{el}=P\cdot t\)
Weitere Formelzeichen für die elektrische Energie sind \(E\) und \(W\). Die elektrische Energie ist eine Form der Arbeit \(W\) (von engl. work).
Die Einheiten der Arbeit / Energie sind \(Ws=J\). In der Elektrotechnik wird elektrische Energie in \(kWh\) statt in \(Ws\) angegeben. Hierfür muß die Einheit erst umgerechnet werden.
Aufgabe 5
Elektrische Energie wird zur Verfügung gestellt, damit sie Arbeit verrichten kann (z. B. Heizarbeit bei einem Elektroherd, mechanische Arbeit bei einer Bohrmaschine). Physikalisch sind Arbeit und Energie dasselbe. Die elektrische Arbeit wird mit dem Elektrizitätszähler (auch nur als Zähler bezeichnet) gemessen.
An einer Normalkochplatte können durch die 7- Takt- Schaltung folgende Heizleistungen erreicht werden:
1. \(P_1=135\ W\)
2. \(P_2=220\ W\)
3. \(P_3=330\ W\)
4. \(P_4=850\ W\)
5. \(P_5=1150\ W\)
6. \(P_6= 1500\ W\)
Die Kochplatte wird an einer Spannung von \(U=230\ V\) betrieben. Berechne die Heizstufen 1-6 die Stromaufnahme.
geg: \(U=230V\), \(P_1-P6\)
ges: \(I_1-I_6\)
Lös: Die Grundformel ist \(P=U\cdot I\), umgestellt nach \(I\) ist es \(I=\frac{P}{U}\)
\(I_1=\frac{P_1}{U}=\frac{135\ W}{230\ V}=\frac{135\ V\cdot A}{230 \ V}=\frac{135}{230}\ A=0,59\ A\)
\(I_2=\frac{P_2}{U}=\frac{220\ W}{230\ V}=0,96\ A\)
\(I_3=\frac{330\ W}{230\ V}=1,41\ A\)
\(I_4=\frac{850\ W}{230 \ V}=3,70\ A\)
\(I_5=\frac{1150\ W}{230\ V}=5\ A\)
\(I_6=\frac{1500\ W}{230\ V}=6,52\ A\)
Aufgabe 6
Am selben Herd wird die Kochplatte für \(t=45\ min\) mit der Heizleistung 4 von \(P_4=850\ W\) verwendet. Berechne, welche Energie dafür benötigt wird.
geg: \(t=45\ min\), \(P=850\ W\)
ges: \(W\)
Lös: \(W=P\cdot t=850\ W\cdot 45\ min\)
Die Einheit \(Wmin\) ist nicht üblich. Entweder wir geben es in \(Ws\) oder \(kWh\) an.
Umwandlung zu Ws
\(Wmin\) -> \(Ws\): \(1\ min = 60\ s\)
Somit wird \(W=850\ W\cdot 45\ min=850\ W\cdot 45\cdot 60\ s=2295000\ Ws\)
Umwandlung zu kWh
\(Wmin\) -> \(kWh\): \(1\ h=60\ min\Leftrightarrow\frac{1}{60}\ h = 1\ min\)
Somit wird \(W=850\ W\cdot 45\ min=850\ W\cdot 45\cdot\frac{1}{60}h=637,5\ Wh\)
\(Wh\) -> \(kWh\): \(1\ kWh = 1000\ Wh\Leftrightarrow\frac{1}{1000}\ kWh=1\ Wh\)
Somit wird \(W=637,5\ Wh=637,5\cdot\frac{1}{1000}\ kWh=0,6375\ kWh\approx0,64\ kWh\)
Antw: Der Herd benötigt bei Heizleistung 4 in 45min Energie von \(0,64\ kWh\).
Aufgabe 7
Die Kosten für die Nutzung elektrischer Energie werden durch die Verteilungsnetzbetreiber (VNB) in Rechnung gestellt. Vattenfall verlangt z.B. für private Kunden \(0,23\ \unicode{0x20AC}/kWh\).
Bedenke, dass du immer Tabellen- und Fachbuch nutzen kannst.
Du bist 14 Tage in den Urlaub gefahren und hast vergessen dein Flurlicht auszuschalten. Die Gesamtleistung der Flurbeleuchtung beträgt \(P=150\ W\). Berechne, welche Kosten dir dadurch entstehen.
geg: \(T = 0,23\ \unicode{0x20AC}/kWh\), \(t=14\ d\), \(P=150\ W\)
ges: \(K_A\)
Antw: \(K_A=W\cdot T\)
eine der gegebenen Größen haben wir nun verwendet, es braucht noch eine Formel für W
\(W=P\cdot t\)
ersetzen wir W in der ersten Formel, mit der Gefundenen
\(K_A=W\cdot T=P\cdot t\cdot T=150\ W\cdot 0,23\ \unicode{0x20AC}/kWh\cdot 14\ d\)
Bringen wir 14d in die Einheit h:
\(1\ d= 24\ h\) und somit \(14\ d= 14\cdot 24\ h=336\ h\)
Setzen wir das ein und multiplizieren Leistung und Zeit
\(K_A=0,23\ \texteuro/kWh \cdot 150 W\cdot 336\ h=0,23\ \unicode{0x20AC}/kWh\cdot 50400\ Wh\)
Die Einheit Wh muß nun zu kWh gewandelt werden
\(1\ kWh=1000\ Wh\Leftrightarrow \frac{1}{1000}\ kWh=1\ Wh\)
Wenden wir das an
\(K_A=0,23\ \unicode{0x20AC}/kWh\cdot 50400\cdot{1}{1000}\ kWh=0,23\ \unicode{0x20AC}/kWh\cdot 50,4\ kWh=11,59\ \unicode{0x20AC}\)
Antw: Es entstehen \(11,59\ \unicode{0x20AC}\) Kosten.